Snadné a přesné měření zúžení

Kužel je termín používaný k popisu zúžení předmětu nebo povrchu. Na této stránce se seznámíte se základy kuželů, včetně jejich účelu, typů součástí, které je používají, metod jejich výpočtu, způsobu výroby a běžných problémů a řešení spojených s jejich měřením.
- Kužely
- Díly, kde se používá zúžení
- Výpočet úhlu zúžení
- Metody výroby kuželů
- Problémy při konvenčním měření kuželů
- Řešení problémů při měření kuželů
- Shrnutí: Výrazné zlepšení a vyšší efektivita měření kuželů
Kužely
Kužel označuje stav, kdy se průměr, šířka nebo tloušťka dlouhé, úzké struktury směrem ke špičce postupně zmenšuje. Existuje mnoho různých typů kuželových tvarů, které se vybírají podle účelu použití. Kužely se používají ke zpevnění konstrukce nebo k usnadnění montáže a vytvářejí se například lisováním nebo řezáním.
Přidání kuželovitého tvaru do návrhu se nazývá zúžení. Velký úhel zúžení se nazývá ostré zúžení a malý úhel zúžení se nazývá mírné zúžení. Sklon je podobný termín jako zúžení a je nutné používat každý z těchto termínů správně.
Rozdíl mezi zúžením a sklonem
Tvar s úhlem sklonu na obou stranách je kužel, zatímco tvar s úhlem sklonu na jedné straně, zatímco druhá strana je rovná, je sklon. Například při pohledu na stejný tvar kruhového kužele, kdy popisujeme sklon jedné strany pouze pomocí středové čáry jako reference, se jedná o sklon. Pokud popisujeme sklon obou stran, pak se jedná o kužel.
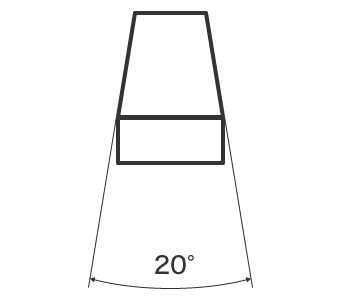
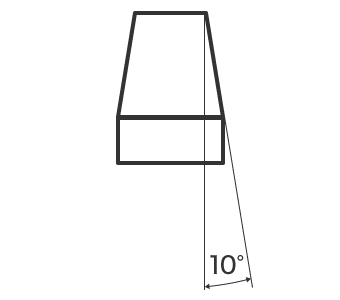
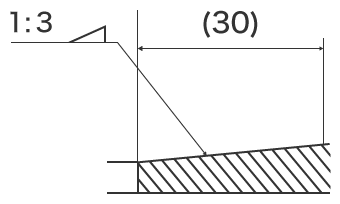
Kreslení notace pro zúžení a sklon
Kužel a sklon jsou označeny symbolem a číselnou hodnotou. Velikost kuželů se udává pomocí úhlu kuželů nebo poměru kuželů. Sklon se označuje číslem, které se nazývá poměr sklonu.
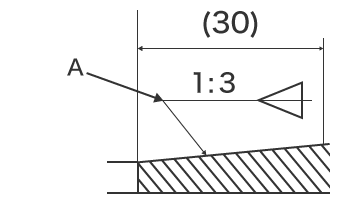
- A
- Symbol kuželosečky zarovnejte ve stejném směru jako tvar kuželosečky.
Díly, kde se používá zúžení
Kužely se používají ve velkém množství dílů, jako jsou ložiska, která podpírají čepy nebo hřídele, trubky a chladiče nebo příruby. Všechny tvary jsou kuželovité, jejich účel je však odlišný a jejich tvary mají různé vlastnosti.
Šrouby, ložiska, montážní díly atd.
Tyto díly používají kužel (lineární kužel), který mění průměr lineárně v závislosti na vzdálenosti. Boční úhel je konstantní a velikost kuželu se udává pomocí úhlu zúžení nebo poměru zúžení.
Chladicí žebra a chladiče motoru
Tyto díly používají kužel (exponenciální kužel), který mění průměr exponenciálně v závislosti na vzdálenosti. Boční tvar se rychleji zužuje ve větší vzdálenosti od základny a špička je velmi ostrá. To umožňuje snížit rozteč a také snížit hmotnost a vibrace.

Kromě toho se kužel s parabolickým tvarem (parabolický kužel) používá u dílů určených ke snížení odporu kapalin, jako jsou potrubí a trupy letadel. U dílů, jako jsou čepy, které se používají ke spojení jiných dílů, se používá obrácený kužel. Obrácený kužel má tvar obrácený oproti běžnému kuželu a jeho špička je silnější než základna.
Výpočet úhlu zúžení
Na výkresech se velikost kuželů obvykle označuje poměrem zúžení. V případech, jako je obrábění na soustruhu, však může být požadována hodnota úhlu zkosení.
Poměr zkosení
Jedná se o poměr rozměru tlustého konce k rozměru tenkého konce. Například při poměru zkosení 3:100 se průměr ztenčí o 3 mm na 100 mm délky.
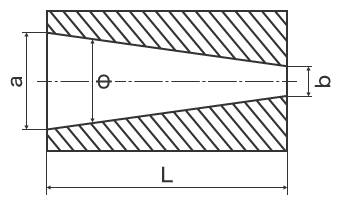
- a
- Větší boční průměr
- b
- Menší boční průměr
- L
- Délka
- Φ
- Úhel zúžení
Úhel zúžení
Úhel zúžení lze vypočítat podle následujícího vzorce.
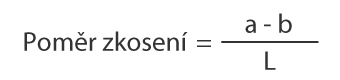
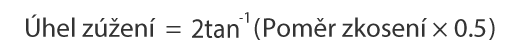
Pokud je například poměr zkosení uvedený na výkresu jako 3/100, lze úhel zkosení vypočítat podle následujícího obrázku.
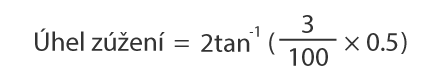
Metody výroby kuželů
Kužely se vytvářejí pomocí soustruhu nebo lisu. Při lisování se při výrobě matrice vytvoří kužel a tento tvar se pak „vtlačí“ do materiálu. V případě soustruhu se obrábění provádí nastavením úhlu držáku destiček. Zde si představíme, jak se vytváří kužel při použití soustruhu.
Soustruh je obráběcí stroj, který odebírá materiál při otáčení. Při otáčení se na povrch předmětu přikládá destička nebo specializovaný řezný nástroj a materiál se odebírá po obvodu. Protože řezání probíhá za rotace obrobku, je tato metoda vhodná pro obrábění kuželů, jejichž průměr se směrem ke špičce ztenčuje. U soustruhu se úhel kuželové frézy udává jako 1/2 úhlu kuželu. 1/2 úhlu zúžení se rovná úhlu sklonu.
(1) Otočte soustruhem a nastavte úhel.
↓
(2) Ovládejte rukojeť soustruhu a provádějte řezání.
↓
(3) Po dokončení řezání se vracejte zpět, dokud se břit nástroje neuvolní.
↓
(4) Tento postup opakujte, dokud nedosáhnete požadovaného tvaru.
Při použití vysoce přesného soustruhu je možné jemné kuželové obrábění v řádu mikrometrů. Pro kontrolu kvality jsou proto zapotřebí vysoce přesné měřicí přístroje.
Problémy při konvenčním měření kuželů
Je nesmírně důležité potvrdit, že rozměry a tvary vytvořené kuželovým obráběním jsou v tolerancích. Zejména proto, že kuželový kužel je trojrozměrný tvar, je vyžadována vysoká přesnost a kvantitativní 3D měření. Při měření pomocí konvenčních optických komparátorů, systémů pro měření profilů a kuželoměrů však dochází k různým problémům. Mezi tyto problémy mohou patřit obtíže při dosahování přesného měření a odchylky naměřených hodnot.
Problémy při měření kuželů pomocí optického komparátoru

Optický komparátor je typ optického měřicího přístroje s podobným principem měření jako optický mikroskop. Objekt je umístěn na podložce a měřicí přístroj vysílá světlo zespodu, čímž promítá profil cíle na obrazovku. Některé velké optické komparátory mají průměr obrazovky větší než 1 m. U dílů se zapuštěnými kužely nelze profil touto metodou zobrazit bez předchozího rozřezání vzorku.
Tato metoda měření zahrnuje následující problémy.
- U běžného optického komparátoru je zaostřena pouze část cíle. Z tohoto důvodu je nutné přesně zaměřit každý měřicí bod ručně. Pokud je například cílem kruhový kužel, je nutné přesně nastavit zaostření v každém místě měření. Z toho vyplývá nejen problém chyby měření, kdy se poloha zaostření liší v závislosti na operátorovi, ale také problém delší doby potřebné k nastavení zaostření při měření více míst. Pro měření tvaru průřezu může být také nutné cíl rozříznout.
- Při porovnávání tvarů je nutné vizuálně zkontrolovat rozdíly překrytím projekce 10× zvětšeným výkresem. Rozdíly mezi promítnutými rozměry a výkresem nelze získat v číselné podobě a tvar profilu se musí přenést na křídový papír, což ztěžuje ukládání a porovnávání dat.
Z toho vyplývá řada velkých problémů. Ne všichni operátoři na místě jsou schopni přesně měřit tvary. Existují také místa, která nelze změřit, a může být nutné cíl rozříznout.
Problémy při měření kuželů pomocí systému pro měření profilů

Systém pro měření profilů měří a zaznamenává profil cíle sledováním jeho povrchu pomocí stylusu. V posledních letech byly vyvinuty systémy pro měření profilů, které používají k měření složitých tvarů bezkontaktním trasováním profilu laser místo stylusu. Některé modely jsou dokonce schopny měřit horní i spodní povrch.
Systém pro měření profilů musí sledovat přesnou měřicí linii v kolmém směru vzhledem k cílovému tvaru kuželu.
To zahrnuje následující problémy.

- Měření vyžaduje mnoho času, včetně času na upevnění vzorku na přípravek a jeho vyrovnání. K přesnému vyrovnání cíle jsou rovněž zapotřebí znalosti a dovednosti související s používáním systémů pro měření profilů.
- Stylus systému pro měření profilů se pohybuje nahoru a dolů v oblouku se středem v opěrném bodě ramene stylusu a hrot stylusu se pohybuje také ve směru osy X. To vede k chybám v údajích o ose X.
- Obkreslení požadované čáry pomocí stylusu je nesmírně obtížná práce a i malé posunutí stylusu způsobuje chyby v naměřených hodnotách.
Řešení problémů při měření kuželů
Z přehledu problémů konvenčních měřicích přístrojů vyplývá, že všechny problémy mají určitý společný bod. To znamená, že měření trojrozměrného cíle nebo plochy se provádí pomocí bodového a liniového kontaktu.
Pro řešení těchto problémů s měřením vyvinula společnost KEYENCE optický 3D profilometr řady VR. Řada VR přesně zachycuje 3D tvar celého povrchu cíle, aniž by došlo ke kontaktu s ním. Měří také 3D tvar pomocí 3D skenování cíle na podložce, a to již za jednu sekundu a s vysokou přesností. To umožňuje okamžité kvantitativní měření, při kterém nedochází k odchylkám výsledků měření. Některé konkrétní příklady výhod jsou vysvětleny níže.
Výhoda 1: Měření bez řezání cíle
Protože sonda nedosáhne až na dno, je u kontaktního měřicího přístroje obtížné měřit cíle s malou roztečí a prohlubněmi, jako jsou nástroje lopatek a žebra chladiče.
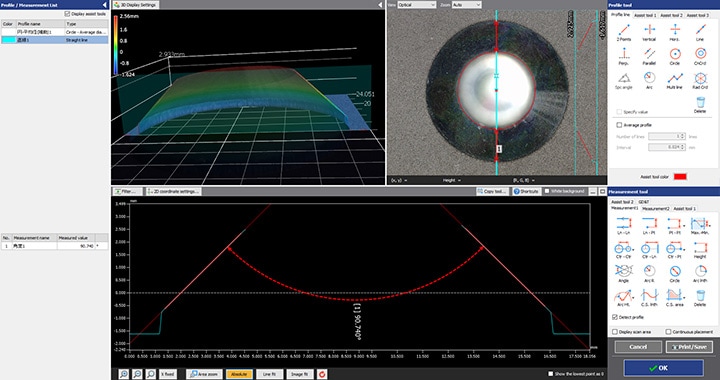
Řada VR dokáže měřit kužely a další tvary virtuálním průřezem objektu, což dříve vyžadovalo skutečné řezání objektu. Dokonce i objekty se zapuštěnými oblastmi lze měřit, aniž by došlo k jejich zničení.
Uživatelé mohou také vytvářet šablony pro běžně měřené položky, aby zefektivnili proces měření a rychle analyzovali více dílů.
Výhoda 2: Měření plochy velké až 300 mm × 150 mm
Měření lze provádět jednoduše umístěním cíle na podložku a stisknutím tlačítka. Přesné polohování ani jiná příprava nejsou nutné. Řada VR je schopna extrahovat prvky z objektu a automaticky upravit zarovnání dílu. To umožňuje provádění vysoce přesných měření i operátorům, kteří nemají znalosti nebo zkušenosti s měřicími přístroji.

Shrnutí: Výrazné zlepšení a vyšší efektivita měření kuželů
Řada VR řeší problémy, se kterými se potýkají konvenční měřicí přístroje, okamžitým měřením 3D objektů pomocí vysoce přesného bezkontaktního 3D skenování.
- Měření průřezů bez řezání cíle.
- Eliminuje odchylky způsobené lidským faktorem a umožňuje skutečné kvantitativní měření.
- Bez nutnosti polohování či jiné přípravy lze měření provést pouhým umístěním cíle na podložku a stisknutím tlačítka. Díky tomu není pro měřicí práce nutné přidělovat specializovanou obsluhu.
- 3D tvary lze měřit snadno vysokou rychlostí a s vysokou přesností. To umožňuje měřit velký počet cílů v krátkém čase, což přispívá ke zlepšení kvality.
Tento systém také umožňuje porovnání s předchozími 3D měřeními a daty CAD a snadnou analýzu dat, například rozložení v rámci tolerancí. Lze jej efektivně využít pro širokou škálu účelů včetně vývoje produktů, analýzy výrobních trendů a kontroly vzorků.